关于分布式系统中一致性的相关概念
一致性这个词出现的场合
ACID 中的 consistency。这个主要涉及数据库的事务或者分布式事务,涉及多个操作之间的顺序。
Raft 或者 Paxos 中的 consensus。这更更多地理解成共识,一致的意见。
MESI cache 一致性协议中的 coherence。这个是设涉及CPU、缓存、主存之间更新数据,涉及读写屏障等。
CAP Theory中的 consistency。这个是讨论存在多份数据和并发访问的情况下可能返回的结果。也是我们这篇文章主要阐述的内容。
分布式系统中一致性的模型
此处的一致性模型又分为聚焦在同时存在多个客户端时的操作顺序,和,以客户端为中心聚焦单个客户端如何与系统交互。
多客户端
严格一致性
strict consistency。
任何进程的任何写入都可以立被任何进程的后续的读操作读取。
这只是一个理论模型。参见Strong consistency models片段。引用部分如下:
在几乎所有真实的 system 中,processes 之间是存在距离的。比如说,内存中一个未缓存的值,在 DIMM(Dual Inline Memory Module) 中可能距离 CPU 30厘米远。我们的 light 需要花费整整一纳秒的时间来走过这段距离(真实的内存访问会更加慢)
https://blog.staynoob.cn/post/2019/03/strong-consistency-model/
上面是国内译作,下面贴原文
in almost every real-world system, processes are distant from each other. An uncached value in memory, for instance, is likely on a DIMM thirty centimeters away from the CPU. It takes light over a full nanosecond to travel that distance–and real memory accesses are much slower.
可线性化
linearizability。又称atomic consistency。
Linearizability: A Correctness Condition for Concurrent Objects https://cs.brown.edu/~mph/HerlihyW90/p463-herlihy.pdf
如果我们假设所有的 processes 都与一个全局的状态对话,并且所有 operation 对该状态中心的影响是原子级的,对彼此之间没有依赖。在这些规则下我们可以排除掉很多可能的 histories。我们知道每个 operation 都会在它的调用时间与返回时间之间的某个时间点生效。
我们称这种一致性模型为线性一致性,因为尽管 operations 是并发的,而且需要时间来完成,但是它们总是有可能能保持一个合理的线性顺序的。
线性一致性是一种非常强壮的模型,一旦一个 operation 完成,所有人都能看到它的结果(或者一些更新的结果),因为所有的 operation 都会在它完成前生效,并且后续调用的 operation 肯定会在调用的时间点后生效。这就意味着一旦我们成功的写入了 b,所有后续的读取操作都会看到 b(或者如果发生了其它的写入,我们会看到比 b 更新的值)。
举例:A在10:00操作了x从1变成2,一旦有一个读者B在10:01读到了x为2,那么C和其他读者在10:01之后读到x必须是2或者更新一点的值,不能是1。
可线性化最重要的一个特征是可见性:一旦操作完成,每个参与者都必须能看到他,并且系统不能穿越到过去。也就是禁止读取过时数据(stale read),他要求读取是单调的。
虽说操作不是瞬时的,但是结果必须在某个时间点变得可见。造成瞬时的错觉。这个时刻称为线性化点(linearization point)。
在并发编程中,可以用cas操作引入可线性化。
在分布式系统中,可线性化需要协调冲突和顺序。它可以使用共识算法实现。共识模块负责确保应用的操作在整个集群中是一致且相同的。
可线性化是最强的单对象、单操作一致性模型。好多场合强一致性是指可线性化。
顺序一致性
sequential consistency。
要求多个写操作全局有序。单个读者看到的写操作的顺序相同。但是并不要求有一个读者读到新值后,其他读者必须读到新值,只要不发生单个读者读到新值后再读到旧值就可以了。
举例:A在10:00操作了x从1变成2,一旦有一个读者B在10:01读到了x为2,那么C和其他读者在10:02读到x可以是1,然后在10:03分再读到x为2,这样是可以接受的(线性一致性不能接受这种),但是不能在10:04又读到x为1(假设x一直没有更新)。
因果一致性
causal consistency。
所有过程必须以相同的顺序看到因果相关的操作。没有因果关系的并发写入可以被不同的进程以不同的顺序观察到。换句话说,即在逻辑上建立了发生在前(happened-before)的关系,而不使用物理时钟,且所有进程都认同这个顺序。
最终一致性
eventual consistency。
最终是一个有趣的术语,因为他没有指定它必须发生的硬性时间限制。这听起来很不可靠,然而实践中这个模型工作的很好。
单客户端
流水线随机访问存储器一致性
Pipelined RAM一致性,也称为FIFO一致性。
- 单调读(monotonic read),如果read(x)已经观察到值v,那么接下来的读必须观察到与v一样新或者某个再新的值。
- 单调写(monotonic write),假设同一客户端以v1 v2的操作写入,那么必须以相同的顺序对所有其他进程可见。如果没有这种假设,旧数据可能复活导致数据丢失。
- 读自己(read-own(your)-write),该模型声明当写操作完成后,每个读操作必须能观察到写入的值。
将单调读(monotonic read),单调写(monotonic write)和读自己(read-own(your)-write)结合起来,可以提供流水线随机访问存储器(PRAM)一致性。
会话因果关系
读后写(write-follow-read)有时也称为会话因果关系。
例:如果write(x,v2)操作排在返回v1的read(x)操作之后,则write(x,v2)将排在write(x,v1)之后。
总结
Consistency Models 这个文档中的图很清楚的展示了多种模型,贴一个国内同学转载的图如下:
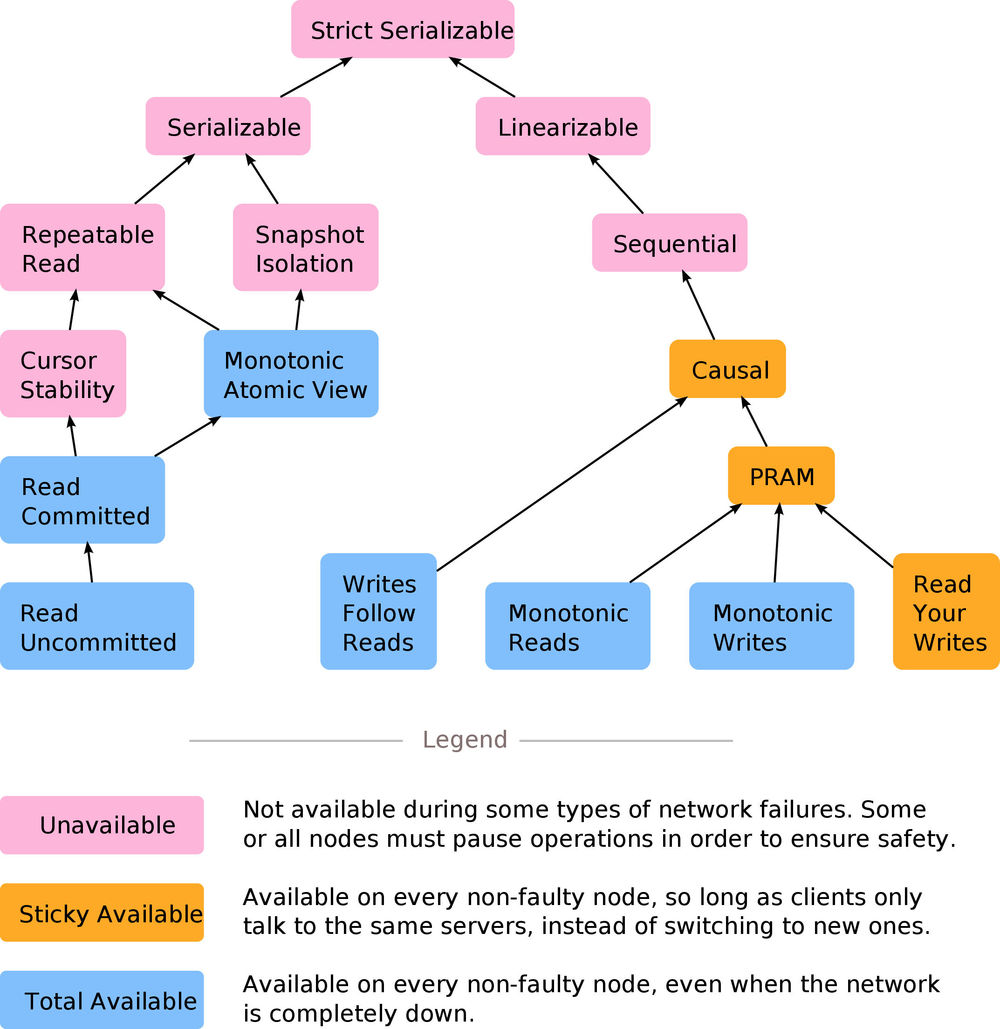
强弱一致性
一致性模型之间的「强弱」比较,是一个相对的概念。比如,线性一致性是比顺序一致性更强的一致性模型。
通常人们把线性一致性称为「强一致性」,把最终一致性称为「弱一致性」,但线性一致性和最终一致性其实存在本质的区别。严格来说,它们并不是一个范畴的概念。
偏序与全序
译《Time, Clocks, and the Ordering of Events in a Distributed System》
Time, Clocks, and the Ordering of Events in a Distributed System
这篇论文主要讲述:一个事件发生在另一个事件之前(happening-before)是一个偏序关系。此篇论文描述了一个算法,让其达成全序关系。
算法的核心部分如下:
现在让我们假设这些进程是一些算法,事件表示算法执行过程中的一些行为。我们将如何进入满足Clock Condition的时钟。进程Pi的时钟由Ci表示,Ci表示Pi中a发生的时间,Ci的值在发生事件时会改变,Ci的改变本身不包含事件。
为了满足Clock Condition,我们需要确保满足C1、C2条件。C1非常简单,进程只需要按照以下步骤:
IR1:任何一个进程Pi在两个成功事件之间递增Ci
为了满足C2,我们需要每条消息m包含一个时间戳Tm,Tm表示消息被发送的时间。收到该消息的进程需要将时钟调整到大于Tm。更准确的,需要满足一下规则:
IR2:(a) 如果事件a表示Pi进程发送消息m,那么m包含一个时间戳Tm,Tm=Ci。(b)进程Pj收到消息m,Pj需要将Cj设置为等于或大于当前值,且大于Tm的值。
在IR2中,我们认为代表消息m被接收的时间在设置Cj之后(其实含义是需要将时间进行调整,之后再处理这条消息)。很明显,IR2保证了条件C2的满足。因此,IR1和IR2保证了Clock Condition的满足,这样它们就保证了得到的是一个正确的逻辑时钟系统。
大意理解成,每个进程独立计数,当受到别的进程的消息时,把自己计数器的大小和消息带过来的对方进程的计数器值比较,取大的作为当前计数器的值。
关于偏序和全序,参见离散数学课本。涉及的概念比较多,我将我的笔记贴一部分如下:
离散数学 邹丽娜 丁茜 罗旭主编
谓词逻辑基本概念
表示个体变元取遍个体论域中的每一个值的量词称为全称量词.例如,“所有的”“一切的”“每一个”“任意的”“凡”“都”等都是全称量词,用符号∀加上一个个体变元表示.如∀x,∀y等都是全称量词,其中,∀表示“全称”,读作“对所有的”,或“对每一个”,而x,y是个体变元.
∀xF(x)表示所有x都具有性质F.
注意:符号∀不能单独使用,其后必须紧跟着一个个体变元.量词∀x作为一个整体看待.
表示个体变元在个体论域中取某个值的量词称为存在量词.例如,表示“存在”“有的”“有些”“有一个”“至少有一个”等都是存在量词.用符号∃加上一个个体变元表示.如∃x,∃y都是存在量词,其中,∃表示“存在”,读作“存在”,或“有这样的”.例如,
∃xF(x)表示存在x具有性质F.
注意:符号∃不能单独使用,其后必须紧跟着一个个体变元.量词∃x作为一个整体看待.
二元关系的定义
定义5-6 设A,B是两个集合,集合R⊆A×B,则称R是A到B的一个二元关系.特别地,若R⊆A×A,则称R是A上的二元关系.
全域关系;IA={<x,x>|x∈A}为A上的恒等关系;∅为A上的空关系.
关系的基本性质
(1)设R是A上的二元关系,若条件∀x(x∈A→<x,x>∈R)成立,则称R在A上是自反的.
例如,当A={a,b,c},R={<a,a>,<a,b>,<b,b>,<c,c>}时,R在A上是自反的;而当B={a,b,c,d,e},R={<a,a>,<a,b>,<b,b>,<c,c>}时,R在B上不是自反的,因为R中还缺少<d,d>和<e,e>.
设R是A上的二元关系,若条件∀x(x∈A→<x,x>∉R)成立,则称R在A上是反自反的.
设R是A上的二元关系,若条件∀x∀y(<x,y>∈R→<y,x>∈R)成立,则称R在A上是对称的.
设R是A上的二元关系,若条件∀x∀y(<x,y>∈R∧<y,x>∈R→x=y)成立,则称R在A上是反对称的.
偏序关系的概念
定义5-21 设R是A上的二元关系,若R是自反的、反对称的和传递的,则称R为A上的偏序关系,简称偏序.常用记号≤来表示偏序关系.若<x,y>∈≤,则记为x≤y,读作“x小于等于y”(或“y大于等于x”).
注意:式子x≤y中符号≤的意义并不是表面上的“小于等于”,而是代表具体意义下的前后顺序关系.例如,在整除偏序关系中,x≤y表示前面x能被后面的y整除;在包含偏序关系中,x≤y表示前面x包含于后面的y;在大于等于偏序关系中,x≤y表示前面x大于等于后面的y.
定义5-22 称一个非空集合A和A上的一个偏序关系≤组成的有序二元租<A,≤>为一个偏序集.
设R是A上的二元关系,若R是自反的、反对称的和传递的,则称R为A上的偏序关系,简称偏序.常用记号≤来表示偏序关系.若<x,y>∈≤,则记为x≤y,读作“x小于等于y”(或“y大于等于x”).
定义5-22 称一个非空集合A和A上的一个偏序关系≤组成的有序二元租<A,≤>为一个偏序集.
例如,整数集Z和Z上的整除偏序关系≤可以构成一个偏序集,即<Z,≤>.
定义5-23 设<A,≤>为一个偏序集,若对于∀x,y∈A,如果x≤y或y≤x,则称x和y是可比的.若x和y是可比的,且x<y(即x≤y∧x≠y),但不存在z∈A,使得x<z<y,则称y是x的覆盖.
例如,由整数和整除偏序关系构成的偏序集中,符合偏序关系的两个元素是可比的,如2和4是可比的(因为2能被4整除,即2≤4成立),3和5是不可比的(因为3不能被5整除,即3≤5不成立).4覆盖2,而虽然2≤8成立,但是8没有覆盖2(因为存在中间的元素4,使得2≤4≤8).
整数集Z和Z上的整除偏序关系≤可以构成一个偏序集,即<Z,≤>.
定义5-23 设<A,≤>为一个偏序集,若对于∀x,y∈A,如果x≤y或y≤x,则称x和y是可比的.
如2和4是可比的(因为2能被4整除,即2≤4成立
4覆盖2,而虽然2≤8成立,但是8没有覆盖2(因为存在中间的元素4,使得2≤4≤8).
定义5-26 设R是非空集合A上的偏序关系,若对任意的x,y∈A,x与y是可比的,即x≤y或y≤x,则称R为A上的全序关系(或线序关系),简称为全序(或线序).
例如,整数集上的“小于等于关系”是一个全序关系;但是,整除关系只是一个偏序关系,而不是一个全序关系.
一些易混淆的概念
关于线性性(Linearizability) 跟可序列化(Serialization) 的关系。这两者看起来似乎相同,然而却是完全不同的两个概念。可序列化(Serialization) 的定义来自于数据库领域,是针对事务的概念,描述对一组事务的执行效果等同于某种串行的执行,没有 ordering 的概念;而 Linearizability 来自于并行计算领域,描述了针对某种数据结构的操作所表现出的顺序特征。// Linearizability是指操作单一object。Serialization可能操作多个object。
关于使用 2PC 来保证线性一致性的说法。2PC 和 3PC 是分布式事务领域的概念,是用来实现分布式事务,而事务的存在主要是保证数据库本身的内部一致性。Linearizability 在前文强调过,是针对 single-object 以及 single-operation 的模型而定义。所以这种说法在描述上并不准确。关于如何实现 Linearizability,可以采用 Active Replication 或 Chain-replication 的系统模型。
注意区可线性化(Linearizability)、可序列化(Serialization)、顺序一致性(Sequential Consistency) 的关系。
本博客所有文章除特别声明外,均采用 CC BY-SA 3.0协议 。转载请注明出处!